Процессы гальванопокрытий и химической обработки деталей находятся в ряду наиболее интенсивных источников загрязнения водных объектов большой гаммой высокотоксичных веществ.

Основной механизм загрязнения – вынос электролитов с промывными водами в межоперационных промывках деталей.

На протяжении более шестидесяти лет множество теоретических и экспериментальных работ в различных странах мира было посвящено созданию рациональных схем, устройств для промывки изделий и методам расчета водопотребления на эти операции.

Наиболее распространенным способом промывки пока остается погружной. С целью сокращения расходов воды на промывку изделий используют многоступенчатые противоточно-каскадные системы промывки.

В работах сотрудников Московского инженерно-экономического института им. Орджоникидзе в 1968–1971 гг. рекомендованы для использования две расчетные формулы для определения расходов воды на промывку применительно к стационарным линиям и автоматам с программным управлением [1, 2, 3, 4]:

,  (1)

,  (2)

Q_min – минимально возможный расход воды на промывку, л/ч;
q – удельный вынос электролита на поверхности изделий из технологической ванны в промывочную, л/м²;
q_час – часовой вынос электролита на поверхности изделий из технологической ванны в промывочную, л/ч;
S – сменная производительность линии по обрабатываемой поверхности изделий, м²/смену;
С₀ – концентрация контролируемого компонента в технологической ванне, мг/л;
С_n – предельно допустимая концентрация контролируемого компонента в промывной воде в момент окончания промывки изделия, мг/л;
n – количество промывок, осуществляемых в промывочной ванне за один час;
V – объем промывочной ванны, л;
N – количество ступеней промывки, N=1;2;3;
8 – продолжительность рабочей смены, ч.

Обе формулы известны как формулы американского профессора Дж. Кушнера. Формула (2) представляет собой упрощенный (приближенный) вариант формулы (1) при

 ,   (3)

где K=C₀/C_n.

Условие (3) является по рекомендациям В.А. Синельникова [1] ограничением для использования формулы (1).

Позднее В.А. Синельников предлагает расширить область применимости формулы (2) для одноступенчатой промывки в соответствии с условием (3) до ≤0,2, но рекомендует в то же время ввести в формулу поправочный коэффициент 1,5, обосновывая его «непредвиденными расходами воды на промывку».

Есть отечественные публикации [5], в которых рекомендуется применение формулы (2) без всяких ограничений и поправочных коэффициентов. Перспектива огромного сокращения потребления воды на промывку изделий обеспечила широкое использование этой формулы для расчета систем промывок, но впоследствии на многих предприятиях качество промывки изделий резко ухудшилось и появился брак в выпускаемой продукции.

К сожалению, во всех последующих рекомендациях, отраслевых руководящих материалах, в ГОСТ 9.047-75, ГОСТ 305-84 и ГОСТ 9.314-90 приводились расчетные методики и номограммы, основанные на формуле (2).

В основу вывода формулы (1) положено условие мгновенного усреднения по всему объему промывочной ванны внесенного в нее с изделием электролита.

Однако, сначала И. Кушнер [6], а затем J.B. Mohler [36, 37] экспериментально показали несоответствие фактического графика изменения концентрации внесенного электролита в промывочной ванне теоретическому, который рассчитывается на основании указанного условия. Но в расчетных формулах это несоответствие не нашло отражения ни в упомянутых работах, ни в последующих выводах Прусака [8] и рекомендациях Смита [9].

Ценные рекомендации по организации системы промывки и конструктивному решению одно- и многоступенчатых ванн промывки даны в работах Н.И. Плотникова [10, 11, 12], а также Веаll и McGathen [13]. Во всех упомянутых работах для уменьшения расхода воды на промывку и улучшения качества промывки рекомендуется применять перемешивание воды в промывочной ванне сжатым воздухом с целью ускорения усреднения электролита в еe объeме. Важным является сделанный Н.И. Плотниковым вывод об обратной зависимости между расходом воды на промывку и количеством промывок в час (при одной и той же часовой производительности).

Таким образом, анализ существующих методов расчета и рекомендаций по организации систем промывки изделий показывает, что слабым звеном, приводящим к занижению расходов воды и недостаточному качеству промывки, является несоответствие теоретических расчетных формул фактической картине изменения концентраций электролита в проточной промывочной ванне.

Нетрудно показать [14], что после внесения в проточную промывочную ванну количества G любого компонента при условии мгновенного усреднения его по всему объему ванны концентрация этого компонента в промывной воде будет уменьшаться по экспоненциальному закону:

, (4)

где C_t– концентрация компонента в воде промывочной ванны в момент времени t, мг/л;
t – время с момента внесения компонента в промывочную ванну, ч;
е – основание натуральных логарифмов.

Закон (4) и условие

 , (5)

отражающее технологические требования к качеству промывки деталей, положены в основу вывода формулы (1).

При периодическом внесении в проточную промывочную ванну с интервалом времени T=1/n количества G компонента концентрация его в промывной воде в соответствии с выражением (4) будет изменяться по ступенчато-экспоненциальному закону (рис. 1).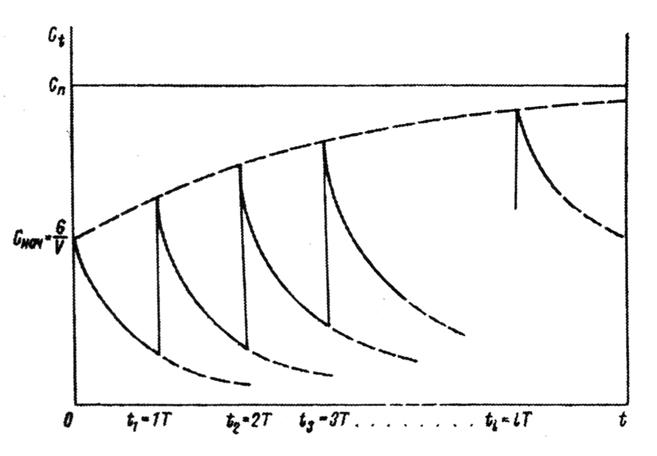
Рис. 1. График изменения концентрации контролируемого компонента в проточной промывочной ванне

Таким образом, подмена формулы (1), отражающей функциональную связь между минимальным необходимым расходом воды на промывку и объемом промывочной ванны, формулой (2), не учитывающей этой связи, приводит к занижению необходимых расходов воды, что подтверждают результаты проверки в промышленных условиях и расчетные данные (табл. 1).

Таблица 1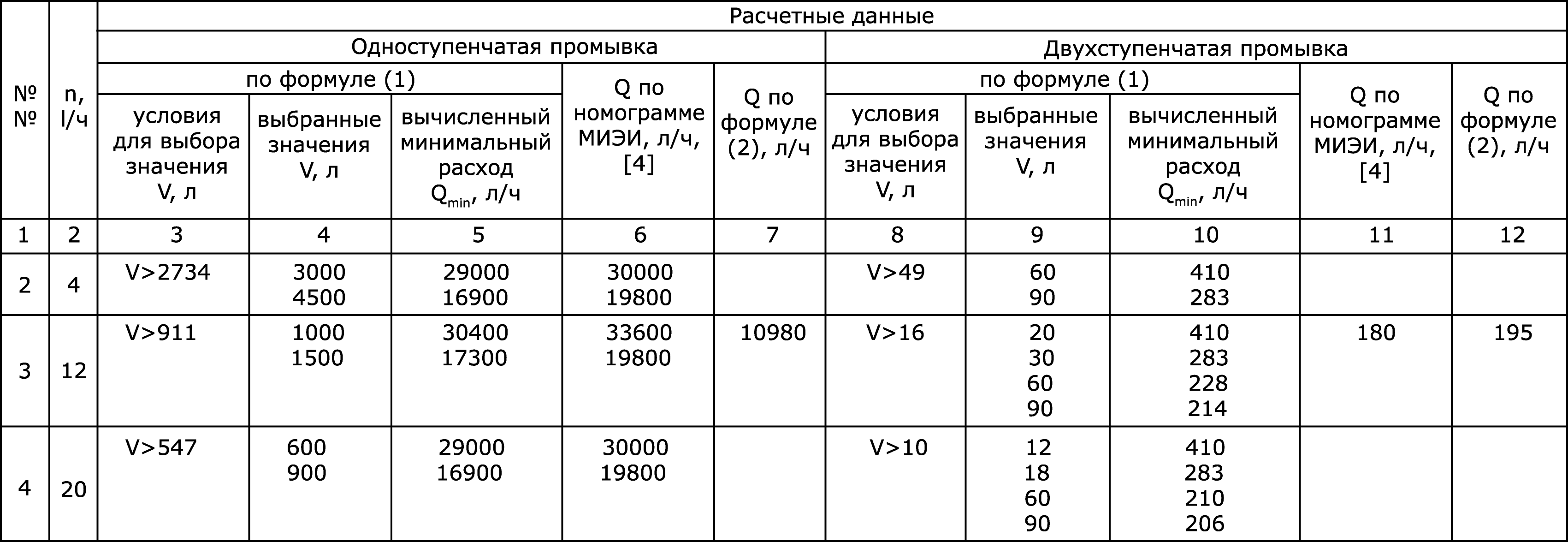

Сравнительные данные по расчету расходов промывных вод 
Исходные данные для расчета: С₀ = 125000 мг/л; С_n = 40 мг/л; q = 0,1 л/м²; S = 280 м²/смену

Незавершенность анализа формулы (1) привела к неправильному толкованию ее на практике. Ошибочно, например, утверждение [3], что уменьшение объемов промывочных ванн и увеличение интервала между промывками (или, что то же самое, уменьшение частоты промывок «n») приводит к уменьшению расхода воды на промывку. В ГОСТ же 9.047 – 75 «Покрытия металлические неорганические» рекомендовалось принимать объемы промывочных ванн минимально возможными («исходя из максимальных размеров одноразовой загрузки» деталей). Ошибочность таких рекомендаций видна по расчетным данным, представленным в таблице 1 и доказывается строго математически.

Так как q, S, С_о и С_n – величины постоянные, то функцию (1) можно представить в виде

, (6)

где    , (N=1, 2, 3) (7)

Функция Qmin как логарифмическая существует только при условии

, (8)

Кроме того, 

, (9)

так как 

Из выражений (8) и (9) следует, что функцию  можно разложить в степенной ряд [15]. Тогда функция Q_min после несложных преобразований примет вид

 (10)

Таким образом, вид полученной функциональной зависимости (10) с неопровержимой очевидностью доказывает обратное положение: минимально возможный расход промывной воды уменьшается с увеличением объема промывочной ванны и частоты промывок.

Если преобразовать выражение (10) к виду

 (11)

то левая часть выражения (11) с учетом (2) и (7) будет представлять отношение минимальных расходов промывной воды, рассчитанных по формулам (1) и (2).

Если теперь учесть, что область существования функции (1) определяется условием

 (12)

то ясно, что при уменьшении «V» в пределе

 , т. к.   и

 (13)

так как в скобках записана сумма членов бесконечного расходящегося ряда [16].

Из выражения (6) следует, что .

Тогда (см. выражение 11) 

  (14)

Отсюда следует, что чем меньше выбирается объем промывочной ванны, тем больше занижается расход промывной воды при расчете по формуле (2) по сравнению с формулой (1); и только при бесконечном увеличении объема ванны это занижение стремится к нулю.

Таким образом, в ГОСТ 9.047 – 75 был рекомендован самый неудачный вариант методики расчета, дающий наибольшие погрешности.

Необходимыми условиями при практическом использовании формулы (1) для расчета двухступенчатой (N=2) и трехступенчатой (N=3) систем противоточной каскадной промывки являются условия назначения объемов промывочных ванн в разных ступенях, которые отсутствуют во всех опубликованных рекомендациях и ГОСТ.

Первое условие (12), общее для всех ступеней и систем с любым количеством ступеней промывки, уже сформулировано.

Второе условие должно отражать соотношение объемов промывочных ванн в разных ступенях. Покажем на примере двухступенчатой противоточной каскадной промывки (рис. 2) получение этого условия.

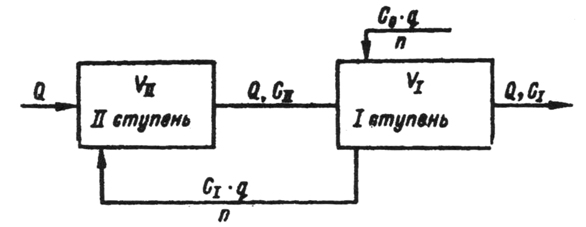Рис. 2. Схема двухступенчатой каскадной противоточной промывки

Необходимый расход воды для обеспечения максимальной концентрации компонента в ванне 2 не более С_n в соответствии с формулой (1) для одноступенчатой промывки составляет:

 (15)

В выражении (15) неизвестной переменной величиной является С_I. Чтобы выразить С_I через известные величины, рассмотрим отдельно ванну I.

Концентрация компонента в ванне I в любой момент времени складывается из концентрации его во входящем из ванны II потоке (С_II) и концентрации, создаваемой периодически вносимыми из технологической ванны порциями электролита. Для первой концентрации пределом служит С_n, вторая концентрация в соответствии с законом (4) имеет предел

 (16)

где  .

Таким образом, в пределе суммарная концентрация компонента в ванне I запишется как

 (17)

Подставив выражение С_I из (17) в (15), получим расчетное уравнение для определения минимального расхода промывной воды, соответствующего этому предельному состоянию системы: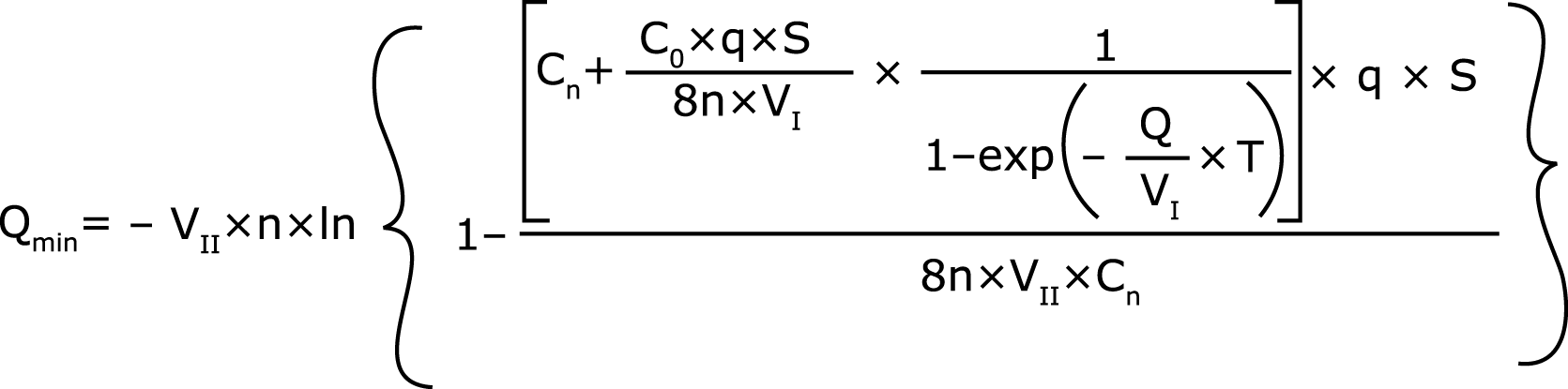 

Анализ уравнения (18) показывает, что оно имеет смысл при условиях

 (19)

V_I>0 (20)

Условие (20) означает, что для выбора объема ванны I могут существовать ограничения только технологического характера. Условие же (19) выполняется при соблюдении условия (12). В то же время уравнение (18) в общем случае является трансцендентным и имеет точное решение только при условии V_I = V_II. Именно при этом условии решением его является выражение (1).

Аналогичная картина имеет место и при трехступенчатой промывке.

Таким образом, использование для расчета уравнения (1) возможно только при равенстве объемов промывочных ванн во всех ступенях промывки.

К сожалению, в последующих ГОСТ 9.305 – 84 «Покрытия металлические и неметаллические неорганические» и ГОСТ 9.314 – 90 «Вода для гальванического производства и схемы промывок» об условиях назначения объемов промывочных ванн не говорится вообще ничего. Кроме того, в последнем ГОСТ методика расчета из «обязательной к применению» стала «рекомендуемой...», очень трудно читается и содержит ряд погрешностей.

Следует отметить, что в начале восьмидесятых годов делались попытки получить расчетные уравнения для определения расходов воды на основе конвекционно-диффузионной модели промывки [17], а также на основе молекулярно-диффузионной и турбулентно-диффузионной модели [18].

Однако, теоретические выводы и экспериментальные данные отражают диффузионные явления на расстояниях 0÷4,5 см от поверхности промываемой детали. И даже эта картина рассматривается при семи допущениях, идеализирующих условия рассматриваемого процесса. В числе этих условий и то, которое лежит в основе вывода уравнений (1) и (2) – «концентрация компонента в промывочном объеме постоянна в любой момент по всей ванне». И несмотря на то, что авторы противопоставляют эти модели подходу Дж. Кушнера, они (модели) еще более далеки от действительной общей картины процесса во всем объеме промывочной ванны. Положительная их роль в том, что они дают представление о механизме и скоростях перехода ионов из пленки электролита на поверхности деталей в окружающие диффузионные слои.

Литература:
1. Синельников В.А. Рациональные системы использования воды в гальвани­ческих цехах машиностроительных предприятий. – В кн.: Материалы семинара «Водоснабжение и канализация предприятий машиностроения». М., МДНТП, 1968 г.
2. Синельников В.А. Исследование системы водоиспользования при промывке изделий в цехах металлопокрытий предприятий машиностроения. Диссертация на соискание ученой степени кандидата технических наук. Горький, 1971 г. 
3. Синельников В.А., Баранов В.В., Трактинский Г.Я. Рациональное использование промывных вод в промышленном производстве. – В кн.: Водоиспользование в промышленности. М., МИЭИ, 1968 г. 
4. Использование воды для промывки изделий в гальваническом производстве. Отраслевые руководящие материалы Министерства станкостроительной и инструментальной промышленности. М., 1970 г. 
5. Гольберг И.Г., Титов Я.Ф., Яремич О.А. Ступенчатая противоточная промывка деталей в гальванических цехах. Л., ЛДНТП, 1969 г. 
6. Kushner J.B. Промывка, загрязнение и естественная рециркуляция гальванических ванн. ч.1. Metall, 1977 г. v.69, №7; ч.II, №8.
7. Mohler J.В. Non – equilibrium Rinsing. Mettall Finishing, 1977 г., v.75, №10; Experimental Rinsing, №12. 
8. Prusar Jakus. Методы расчета расхода воды в гальванических цехах. ч.III. Powloky ochronne, 1977 г. v.5, №6.
9. Smith С.А. Контроль стоков гальванических цехов. ч.1. Water Serv., 1980 г.,84, №1007.
10. Плотников Н.И. Определение расхода воды при промывке изделий в травильных отделениях металлургических заводов. Цветная металлургия, 1965 г., №2.
11. Плотников Н.И. Определение расхода воды при промывке изделий в гальванических цехах. Вестник машиностроения, 1965 г., №7.
12. Плотников Н.И. Определение расходов воды при промывке изделий. Информ. листок, 1964 г., №187, (Новосибирский ЦНТИ).
13. Beall John F., MeGathen Rod. Руководство по очистке сточных вод. ч.1. Как уменьшить объем сточных вод. Metall Finishing, 1977 г., v.75, №9.
14. Батунер Л.М., Позин М.Е. Математические методы в химической технике. ГОСХИМиздат, Л., 1963г.
15. Бронштейн И.Н., Семендяев К.А. Справочник по математике. М., 1957 г.
16. Корн Г., Корн Т. Справочник по математике для научных сотрудников и инже­неров. Издат. «Наука», М., 1970 г.
17. Kubik С. Конвекционно-диффузионная модель промывки. 1. Теория процесса. 2. Экспериментальная проверка. Surface Tehnology, 1981 г., №13.
18. Buczko Z. Математическая модель процесса разбавления в одиночной ванне промывки методом погружения. Powloki ochronne, 1983г., №3.