Практика эксплуатации систем промывки деталей на множестве промышленных предприятий показала, что в очень многих случаях расходы воды, рассчитанные по формуле (1), также оказываются недостаточными для обеспечения требуемого качества промывки.

Объясняется это тем, что на практике мгновенного усреднения электролита по всему объему промывочной ванны не происходит.

В результате исследований установлено, что фактический график изменения концентрации контролируемого компонента в воде промывочной ванны имеет вид, показанный на рис. 3.

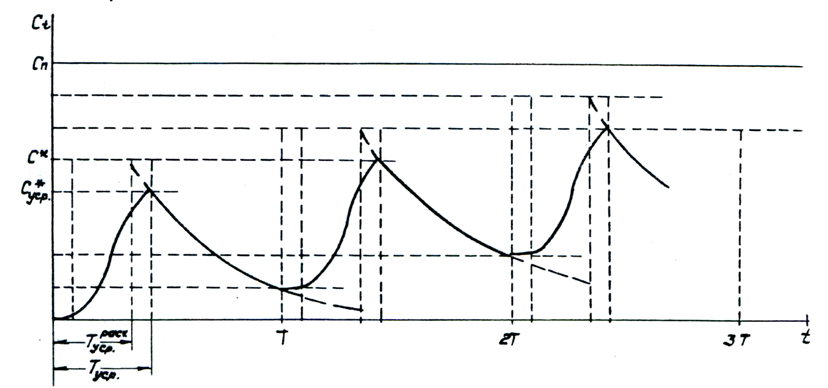
Рис. 3. Фактический график изменения концентрации контролируемого компонента в воде промывочной ванны

Таким образом, с учетом времени усреднения при расчете расхода воды на промывку в уравнение (1) вместо величины n=1/Т, стоящей перед знаком логарифма, должна подставляться величина n=1/(T-T_уср.^{расчет.}) причем, очевидно, что чем большую долю от «Т» составляет величина T_уср.^{расчет.}, тем больше будет необходимый расход воды на промывку.

В связи с этим появляется необходимость в методах расчета времени усредне­ния концентрации компонента в промывочной ванне при использовании барботажного перемешивания.

Основные положения, необходимые для постановки исследований по этому вопросу, на основании изучения литературных данных можно сформулировать следующим образом:

– эффективность перемешивания жидкости воздухом увеличивается с ростом глубины резервуара и уменьшением площади зеркала воды в резервуаре [19, 20, 21, 22, 23, 24];

– интенсивность и время полного перемешивания в сильной степени зависят от расхода воздуха на единицу перемешиваемой жидкости [23, 25];

– высокая вязкость жидкости обусловливает большее увеличение времени полного смешивания при меньших расходах воздуха [20];

– циркуляционный поток в перемешиваемой жидкости в значительной степени зависит от скорости барботирующего газа и величины расхода перемешиваемой жид­кости в аппарате (для случая горизонтального течения жидкости), что проявляется в сильной зависимости коэффициента продольной диффузии от этих параметров [25, 26];

– для перемешивания слоя жидкости высотой 2,7 м необходимо на 1 м² поверхности следующее количество воздуха [19, 21]:

для перемешивания средней интенсивности – 11,9 м³/ч;
для перемешивания интенсивного – 24,1 м³/ч;
для перемешивания очень интенсивного – 60,1 м³/ч,

при высоте слоя жидкости 1 м количество воздуха надо удвоить, чтобы получить ту же интенсивность перемешивания.

На основании изложенных положений, а также изучения ряда работ теоретического и экспериментального характера, связанных прямо или косвенно с решением рассматриваемой задачи, было решено искать эмпирическое уравнение для расчета времени усреднения в зависимости от четырех определяющих независимых параметров:

qв– удельного расхода воздуха при барботировании на 1 м² поверхности в ванне (параметр «а»);
F – площади зеркала воды в промывочной ванне (параметр «b»);
V/Q – времени пребывания промывной воды в промывочной проточной ванне при установленном расходе «Q» (параметр «с»);
G/V – количество вносимого в промывочную ванну за один раз контролируемого компонента, отнесенного к ее объему (параметр «d»).

На основании обследования режимов работы большого числа ванн промывки были намечены интервалы варьирования и уровни варьируемых параметров для проведения экспериментов, которые представлены в таблице 2 (нумерация формул, таблиц, рисунков и литературных источников сохранена в соответствии с частью 1).

Таблица 2

Экспериментальные значения варьируемых параметров на различных уровнях

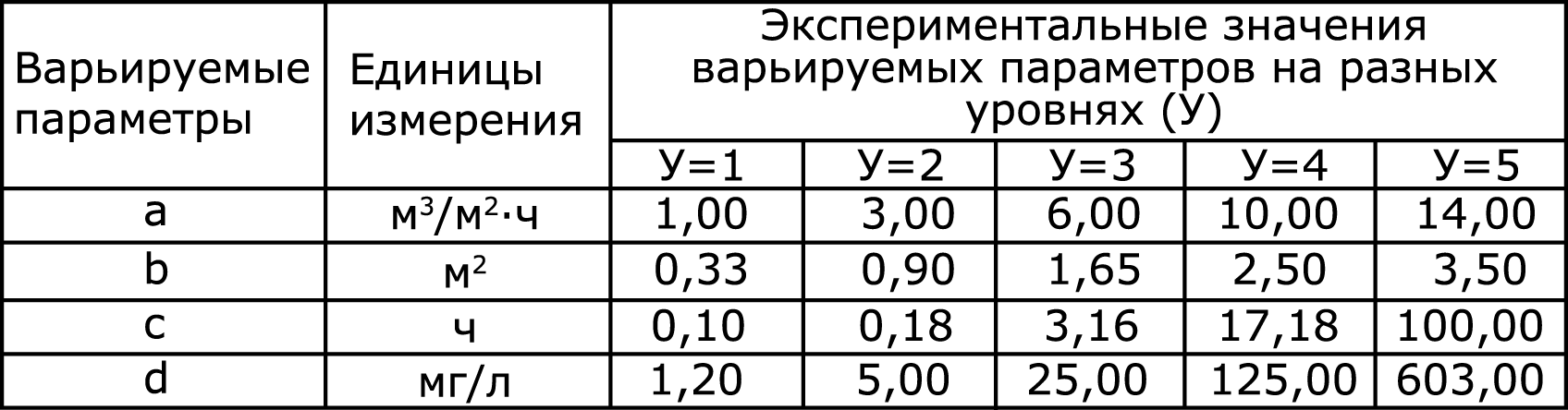
Следует особо оговорить, что максимальное значение параметра «а» ограничено техническими причинами (при более интенсивном барботаже вода выплескивается из ванн), а также экономическими соображениями; минимальное значение параметра «d», оказывающее влияние на время усреднения, как показали предварительные исследования, равно 1,2 мг/л – при дальнейшем уменьшении его значений время усреднения остается постоянным.

Проведение экспериментов для получения интересующей функции планировалось по принципу четырехфакторной классификации в греко-латинском варианте [27].

Методика осуществления экспериментов заключалась в следующем: в центр объема промывочной ванны, заполненной водой, подавалась мгновенно доза раствора серной кислоты, соответствующая в каждом эксперименте запланированному значению параметра «d» (таблица 2); расход промывочной воды через ванну (Q) и воздуха (qв в течение 10 мин. до момента ввода в ванну кислоты и далее в течение всего опыта также соответствовали запланированным значениям «с» и «а»; в момент ввода кислоты в ванну из точек 7 (рис. 4) в средней по глубине зоне со стороны впуска воды в ванну, со стороны выпуска ее из ванны и в центральной части ванны с помощью микронасосов 8 начинался отбор проб жидкости, которая пропускалась через проточные датчики электропроводности, подающие сигналы на показывающие приборы 1 и записывающие устройства 2; временем усреднения (Туср.) концентраций кислоты в объеме ванны считалось время, соответствующее максимальному сближению всех трех снятых кривых изменения электропроводности в точках 7, начиная с которого все три кривые плавно снижаются параллельно друг другу; поскольку за время «Туср.» часть кислоты выносится из ванны с проточной водой и средняя концентрация кислоты в промывной воде к этому моменту снизится до величины «С*уср.», для осуществления расчетов удобно определить время «Туср.расчет.», соответствующее концентрации «С*уср.» (т. е. нулевому выносу кислоты, рис. 3); для этого необходимо определить величину Туср.–Туср.расчет., что можно сделать, логарифмируя выражение (4):

откуда

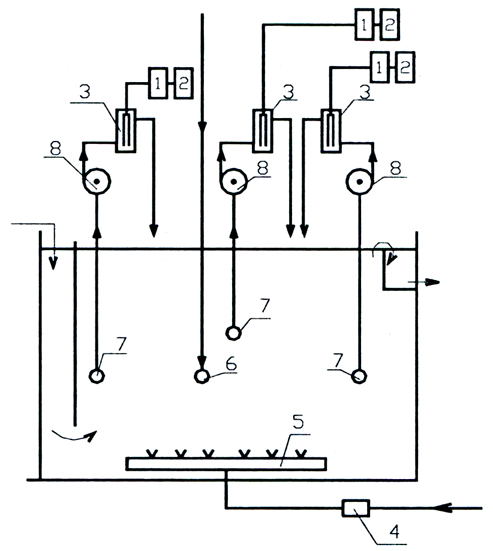
Рис. 4. 1 – вторичные приборы для измерения электропроводности раствора; 2 – записывающие устройства; 3 – проточные датчики электропроводности; 4 – расходомер воздуха; 5 – барботажное устройство; 6 – точка ввода кислоты в ванну; 7 – точки отбора воды для измерения электропроводности; 8 – микронасосы

Концентрация  определялась как средняя между тремя контролируемыми точками ванны по значениям электропроводности в этих точках (прибор был предварительно оттарирован по стандартным растворам серной кислоты).

Условия проведения каждого эксперимента и вычисленные по формуле (22) на основании полученных экспериментальных данных значения «Т_уср.^{расчет.}» представлены в таблице 3 (каждый опыт проводится дважды и по двум результатам высчитывалось среднее значение), соответствующей греко-латинскому квадрату.

В результате математической обработки экспериментальных данных греко-латинского квадрата, выполненной способами «скользящей средней» и «наименьших квадратов», найдены эмпирические формулы, отражающие влияние определяющих независимых параметров:

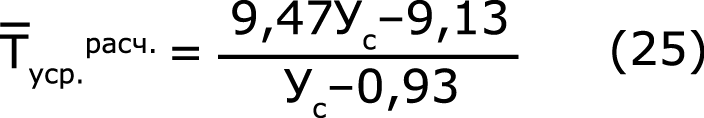
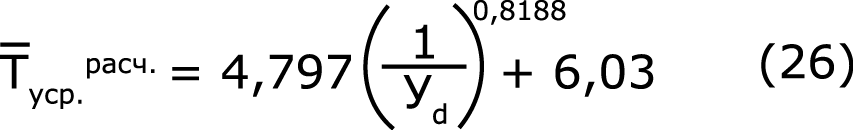
где У_а, У_b, У_c, У_d – экспериментальные уровни соответственно a, b, c, d.

При дальнейшей обработке на основании экспериментальных значений «Т_уср.^{расчет.}» (табл. 3) и частных зависимостей (23÷26) получено общее уравнение регрессии, адекватно описывающее экспериментальные данные через варьируемые параметры:

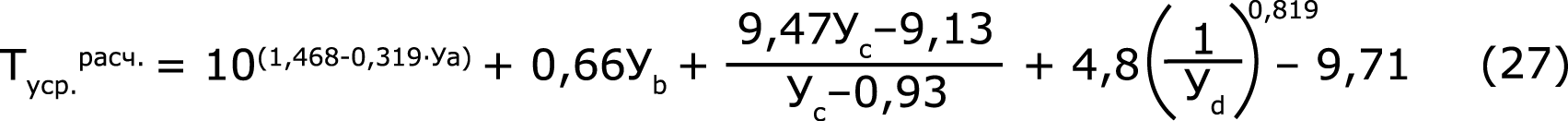
Масштаб каждого параметра определяется выражениями:

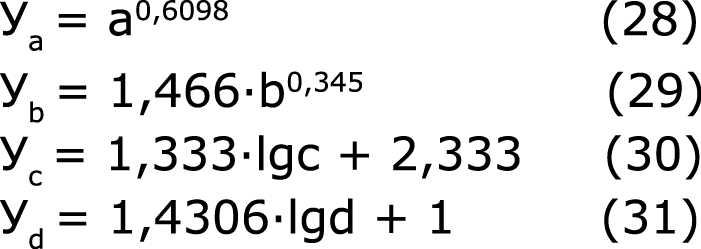
Таблица 3

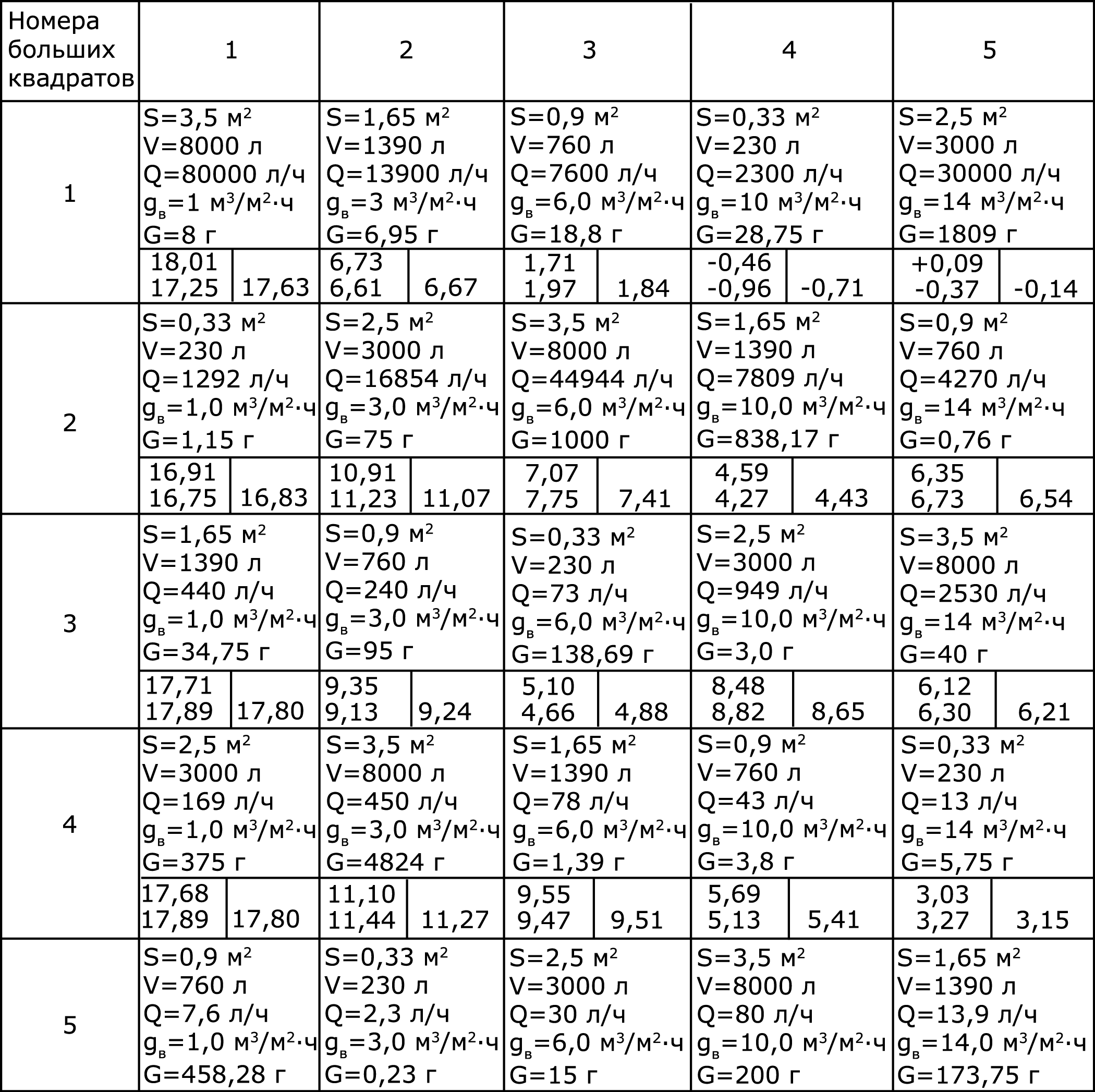
Условия проведения экспериментов и экспериментальные значения Туср.расчет. (мин.)

Функции (28÷31) непрерывны и имеют непрерывные производные. Если на основании отмеченного в выражении (27) заменить переменные в соответствии с выражениями связи (28÷31), перейти к первоначальным обозначениям физических параметров и сделать несложные преобразования, то получим окончательную эмпирическую формулу для расчета величины «Т_уср.^{расчет.}»:

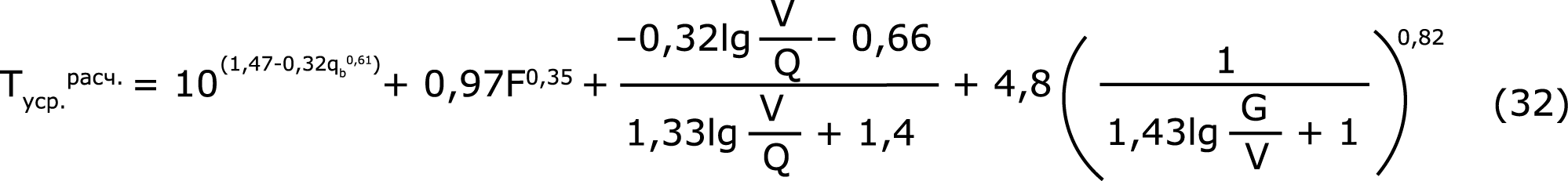
Чтобы получить формулу для расчета «Q_min» с учетом времени усреднения для двухступенчатой системы промывки, запишем выражение (18) с учетом соответствующих поправок для I и II ступеней промывки:

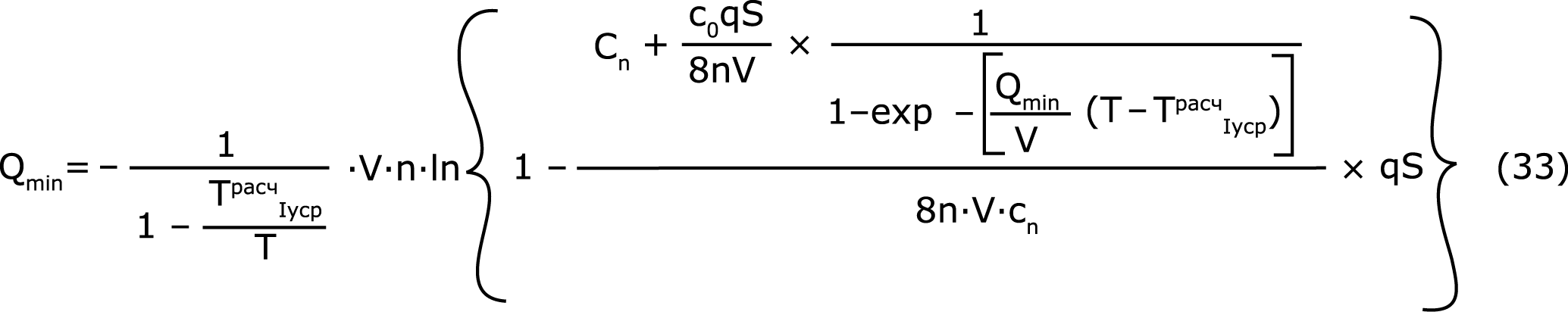
Разделив обе части выражения (33) на 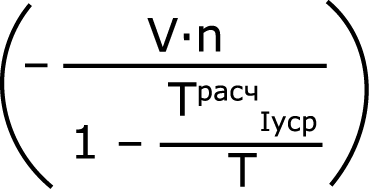, потенцируя и выполнив перегруппировку членов, получим:

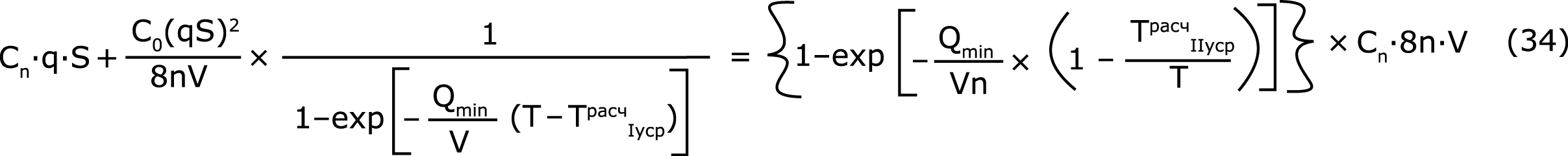
Разделив все члены последнего уравнения на (С_n×q×S) и введя обозначения с₀/c_n=k; _qS/8nV=p получим уравнение

Нетрудно показать, что уравнение (36) не имеет точных способов решения. Решение может быть найдено для малых значений Q_min/V при использовании приближенной формулы ex≈1+x для малых «x» (это соответствует большим значениям «V», т. к. (T_уср.–T_уср.^{расчет.})<1 всегда). В этом случае уравнение (36) преобразуется к виду:

Уравнение (37) имеет один вещественный корень

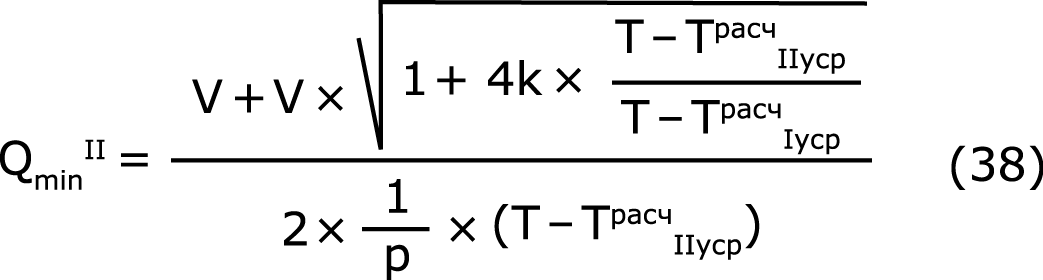
который после упрощения и обратной замены в соответствии с (35) принимает вид:

Сделанное ранее заключение (14) означает [16], что функция (1) асимптотически равна функции (2) при V→∞, а отсюда следует, что решением уравнения (36) для всего допустимого интервала значений «V», которое будет асимптотически равным решению (39) при V→∞, может быть только решение

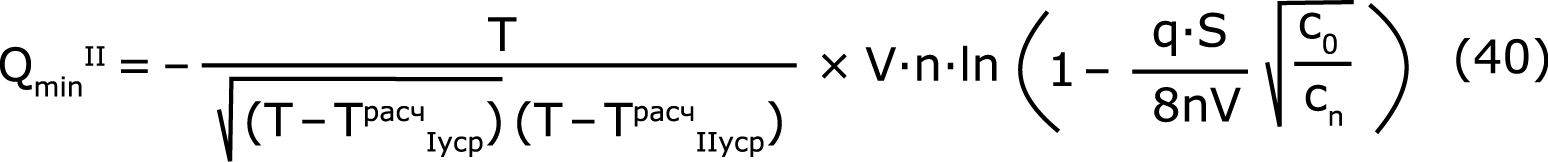
Аналогично выводится формула для расчета «Qmin» с учетом времени усреднения для трехступенчатой промывки

На основании выполненных теоретических и экспериментальных исследований разработаны методики расчета режимов промывки деталей для разных вариантов проектных решений.

При расчете оптимального расхода воды на промывку деталей для существующей системы промывки необходимо:

– определить по исходным технологическим данным теоретический минимально возможный расход воды по формуле (1) – Q_min(T);

– на основании полученного значения Q_min(T) и дополнительных технологических данных – площади зеркала воды в промывочной ванне (F) и удельного расхода воздуха на 1м² поверхности ванны при барботировании q_в – определить для каждой ступени промывки расчетное время усреднения «T_уср.^{расчет.}» по формуле (32); для расчетов по этой формуле следует принимать:

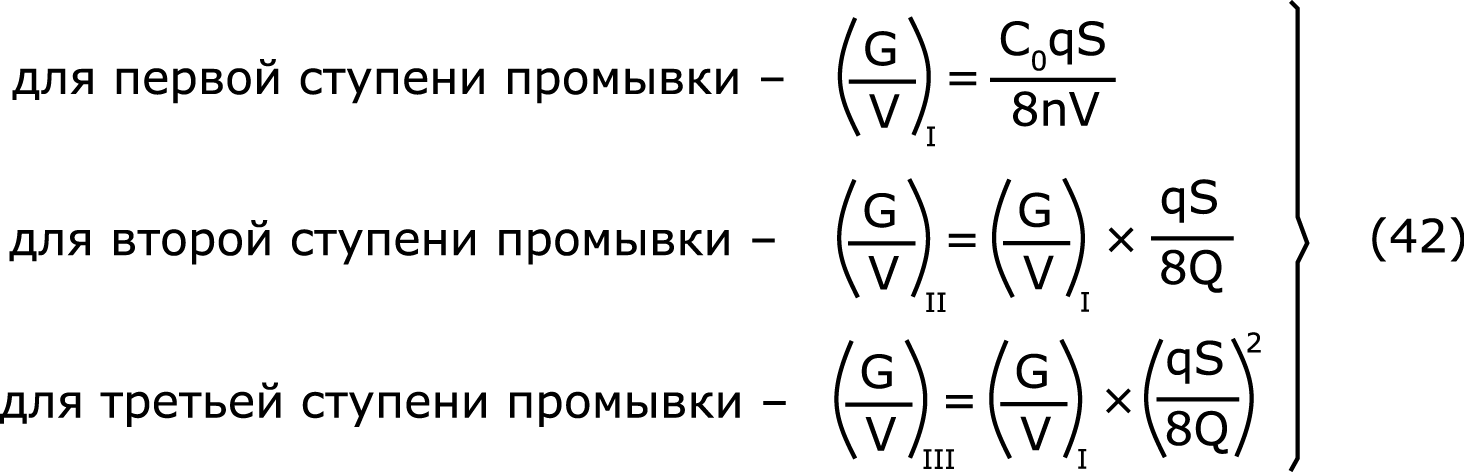
что следует из выводов формулы (1); при значениях G/V менее 1,2 мг/л в расчетную формулу (32) подставляется значение 1,2 мг/л, т. к. дальнейшее уменьшение этого параметра не влияет на время усреднения компонента в объеме ванны;

– определить окончательно минимальный необходимый расход воды на промывку по формуле

Q_min=K_N×Q_Nmin (43)

где K_N – выведенные выше поправочные коэффициенты для систем промывки с разным количеством ступеней (N):

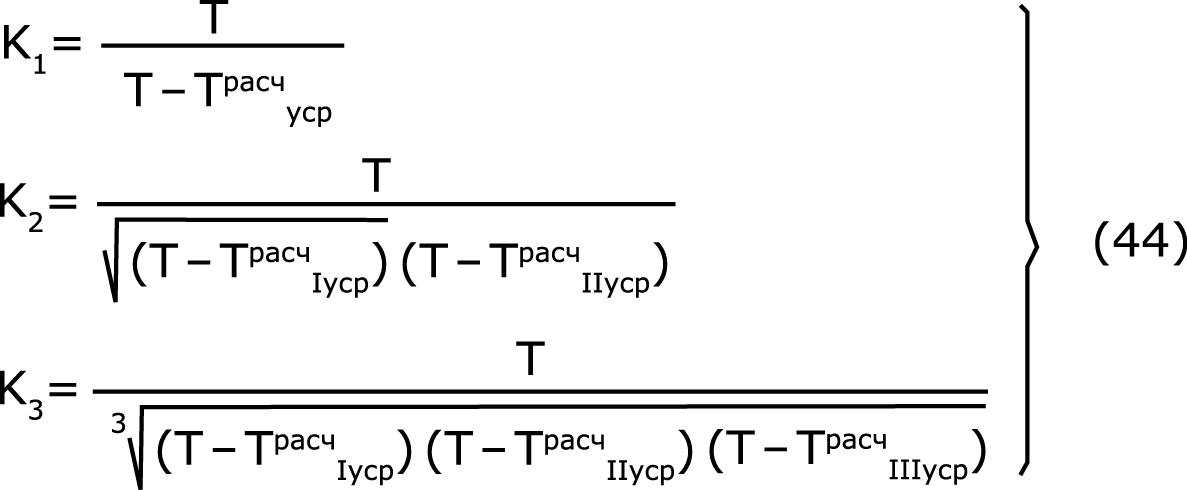
Для упрощения расчетов по формуле (32) построены машинным способом графики для определения всех четырех компонентов, составляющих Tуср.расчет. (рис. 5÷8)

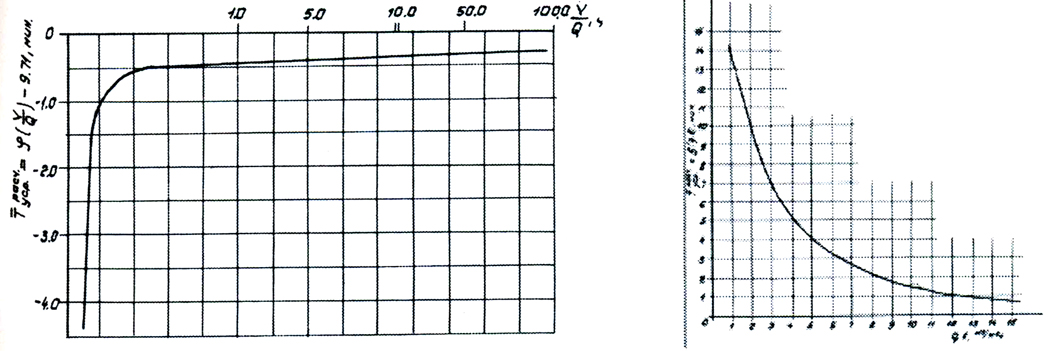
                         Рис. 5. График зависимости Tуср.расчет.=φ(V/Q)                  Рис. 6. График зависимости Tуср.расчет.=f(qb)

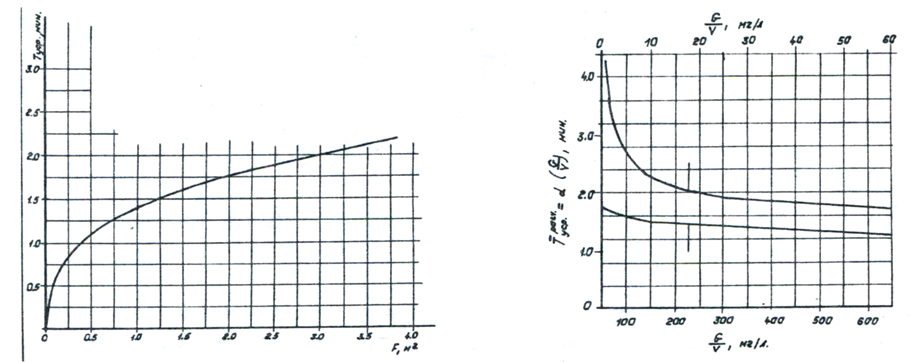
                        Рис. 7. График зависимости Tуср.расчет.=γ(F)                      Рис. 8. График зависимости Tуср.расчет.=α(G/V)

При выборе объемов промывочных ванн необходимо учитывать условие 12.

Нужно иметь также в виду, что эмпирическая формула (32) справедлива в следующих интервалах изменения влияющих параметров: V/Q – 0,1÷100 ч; F – 0,33÷3,5 м²; q_в – 1,0÷14м³/м²ч; G/V – 1,2÷603 мг/дм³.

Литература:

19. Kaufman H.L. Определение расходов воздуха при решении задач смешивания. Chem. and Met.Eng., 1930, 37, N3, стр. 178–180.
20. Perry R.L. Лабораторные исследования смешивания жидкостей с помощью воздуха. «Journal of Dairy Science», 1957, v. 40, p. 1152–1164. 
21. Штербачек З., Тауск П. Перемешивание в химической промышленности: Пер. с чешского. П., Госхимиздат,1963, стр. 246–252.
22. Гандзюк М.П. Исследование процесса перемешивания барботажем: Автореферат диссертации на соискание степени к.т.н. – Киев, 1962, стр. 17–20.
23. Глинков М.А. К вопросу о перемешивании жидкости газовыми пузырями. –Доклады АН СССР, Новая серия, 1946, т. 51, вып. 2, стр. 95–98.
24. Тарнопольская М.Г. Основы расчета смесителей сточных вод: Сб. №4 Очистка промышленных сточных вод, М., Стройиздат, 1968 г., стр. 11–23.
25. Теория и практика перемешивания в жидких средах. Тезисы докладов 2-ой Всесоюзной конф. по теории и практике перемешивания в жидких средах, г. Черкассы, 29 мая – 1 июня 1973 г. НИИТЭХим, М.,1973, стр. 142–145.
26. Тов Б.Г., Брагинский Л.Н., Новичков А.Н., Добросердов Л.Л. Определение коэффициента турбулентной диффузии в аппаратах с барботажным перемешиванием.
27. Прододьяконов М.М., Тедер Р.И. Методика рационального планирования экспериментов. Издат. «Наука», М., 1970.